Hurley's 校招面经

# 查找

# 顺序查找

顺序查找也称为线性查找，属于无序查找算法。它是最简单的查找策略，对于小规模的数据，顺序查找是一个不错的选择。

基本思想是从数据的第一个元素开始，依次比较，直到找到目标数据或查找失败。

  1. 从表中的第一个元素开始，依次与关键字进行比较；
  2. 若某个元素匹配关键字，则查找成功；
  3. 若查找到最后一个元素还未匹配关键字，则查找失败；

时间复杂度：顺序查找平均关键字匹配次数为表长的一半，其时间复杂度为O(n)O(n)。

代码位于：https://github.com/HurleyJames/DataStructure/blob/master/Search/src/SequentialSearch.java

# 有序查找

# 二分查找

二分查找（binary search）也称为折半查找（half-interval search），属于有序查找算法，是一种在有序数组中查找某一特定元素的搜索算法。元素必须是有序的，如果是无序的则要限进行排序操作。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程就结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且同样是从中间元素开始查找（递归）。这样每一次比较都会使搜索范围缩小一半。

时间复杂度：因为正常情况下每次查找的元素都在一半一半地减少，所以二分查找的时间复杂度是log2(n)log_2(n)

代码位于：https://github.com/HurleyJames/DataStructure/blob/master/Search/src/BinarySearch.java

# 插值查找

其实二分查找就是折半，那么为什么不能折四分之一或者其它数字呢？

即二分查找的查找点计算为mid=(low+high)/2mid=(low+high)/2，那么通过类比，可以将查找的点改进为：

mid=low+(key−a[low])/(a[high]−a[low])∗(high−low) mid=low+(key-a[low])/(a[high]-a[low])*(high-low)

基本思想就是基于二分查找的改进，将折半改为自适应，可以提高查找效率。但插值查找的前提也必须是已经有序排列。

代码位于：

# 斐波那契查找

# 线性索引查找

# 哈希查找

# 二叉查找树

二叉查找树（BinarySearch Tree）也叫二叉搜索树，也可以叫二叉排序树（BinarySort Tree），是具有以下性质的二叉树：

  1. 若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若任意节点的右子树不为空，则右子树上所有节点的值均大于它的根节点的值；
  3. 任意节点的左、右子树也分别为二叉查找树；

即 右 > 根 > 左，同时对二叉查找树进行中序遍历，即可得到有序的数列。

使用二叉查找树的思路是：

  • 如果相等，即查找成功；
  • 如果比较结果为根节点的关键字值较大（大了），则说明可能在左子树中；
  • 如果比较结果为根节点的关键字值较小（小了），则说明可能在右子树中；

# 平衡二叉树

平衡二叉树是对二叉查找树的一种改进。二叉查找树有一个明显的缺点就是树的结构仍然具有极大的变动性，最坏的情况下就是一颗单支二叉树，丢失了二叉查找树的一些原有的优点。

平衡二叉树（AVL）：它可以是一颗空树，也可以是具有以下性质的二叉查找树：

它的节点左子树和右子树的深度之差不超过1，而且该节点的左子树和右子树都是一颗平衡二叉树（即同样满足这个性质）。

平衡因子：节点左子树的深度 - 节点右子树的深度。值可以为0、-1、1。

# 红黑树

# 简介

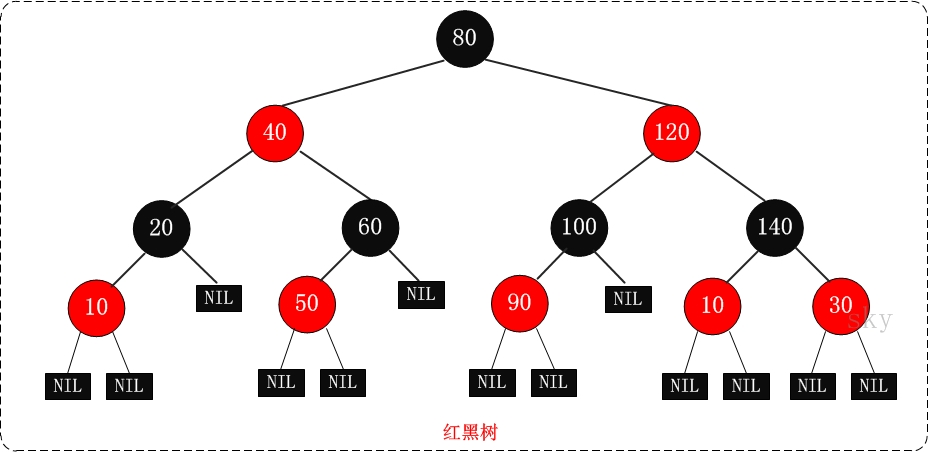
红黑树是一种特殊二叉查找树。红黑树上的每个节点都有存储位以表示节点的颜色，可以是红色也可以是黑色。

其特点有：

  • 每个节点都是黑色或者红色
  • 根节点是黑色
  • 每个叶子节点都是黑色（叶子节点是指为空（NIL或者NULL）的节点）
  • 如果一个节点是红色的，其子节点就是黑色的
  • 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

因为特性5，所以红黑树是一个相对接近平衡的二叉树。

红黑树

# 应用

红黑树主要用来存储有序的数据，它的时间复杂度是O(lgn)O(lg_n)。

Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

# B树和B+树

也称为多路查找树。

← 动态规划 →